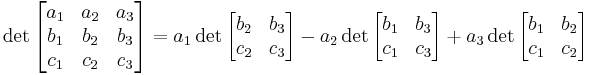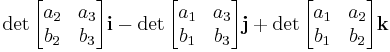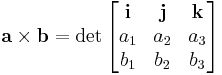Abuse of notation

In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition (while being unlikely to introduce errors or cause confusion). Abuse of notation should be contrasted with misuse of notation, which should be avoided. A related concept is abuse of language or abuse of terminology, when not notation but a term is misused. By an abuse of language, this itself is often referred to as "abuse of notation".

The new use may achieve clarity in the new area in an unexpected way, but it may borrow arguments from the old area that do not carry over, creating a false analogy.

Abuse of language is an almost synonymous expression that is usually used for non-notational abuses. For example, while the word representation properly designates a group homomorphism from a group G to GL(V) where V is a vector space, it is common to call V "a representation of G."

1 Examples
2 Bourbaki
3 Abuse of language or notation?
4 See also
5 References
6 External links

Examples

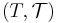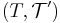Common examples occur when speaking of compound mathematical objects. For example, a topological space consists of a set $T$ and a topology $\mathcal{T}$ , and two topological spaces $(T, \mathcal{T})$ and $(T, \mathcal{T'})$ can be quite different if they have different topologies. Nevertheless, it is common to refer to such a space simply as $T$ when there is no danger of confusion—that is, when it is implicitly clear what topology is being considered. 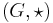Similarly, one often refers to a group $(G, \star)$ as simply $G$ when the group operation is clear from context.

Derivative

In standard analysis, algebraic manipulations of the Leibniz notation for the derivative 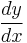$\frac{dy}{dx}$ is commonly thought to be an abuse of notation. It is frequently convenient to treat the expression 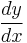$\frac{dy}{dx}$ as a fraction. For example, it leads to the correct formula for differentiation of the composition of functions (commonly called the "chain rule") 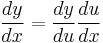$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$ . 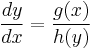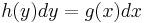Another example is the concept of separation of variables in solving differential equations, in which one can rewrite the equation $\frac{dy}{dx}={g(x) \over h(y)}$ as $h(y) dy = {g(x)dx}$ and then integrate. 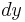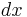However, this treatment does not have to be viewed as an "abuse of notation", because it can be fully justified by taking the "differentials" ${dy}$ and ${dx}$ as simply being two numbers in the ratio 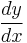$\frac{dy}{dx}$ : 1. If this is done, then the methods are completely rigorous, with no "abuse of notation" involved. In terms of a graph of $y$ against $x$ , this can be thought of as taking d $x$ and d $y$ as the horizontal and vertical components of a vector along a segment of a tangent to the graph. Leibniz's own interpretation was of a ratio of infinitesimal changes in $x$ and $y$ , and a similar interpretation occurs in non-standard analysis, but in standard analysis no such "infinitesimals" are needed, as finite real numbers provide a fully rigorous justification.

Del operator

The del operator, denoted by 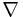$\nabla$ , is a tuple of partial derivative operators posing as a vector. This suggests notations such as 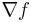$\nabla f$ for gradient, 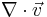$\nabla \cdot \vec v$ for divergence and 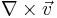$\nabla \times \vec v$ for curl. The notation is extremely convenient because 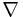$\nabla$ does behave like a vector most of the time. But it can be regarded as an abuse because 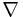$\nabla$ doesn't commute with vectors, and so doesn't satisfy all properties of vectors.

(A contrary view is that notation is not abused if one does not think of 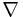$\nabla$ as a vector. The vector-like notations are simply specially defined uses of the dot and cross.)

Cross product

The determinant of a 3×3 matrix may be computed by "expanding along the first row" as follows:

$\det \begin{bmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{bmatrix} = a_1 \det \begin{bmatrix} b_2 & b_3 \\ c_2 & c_3\end{bmatrix}- a_2 \det \begin{bmatrix} b_1 & b_3 \\ c_1 & c_3\end{bmatrix}%2B a_3 \det \begin{bmatrix} b_1 & b_2 \\ c_1 & c_2\end{bmatrix}$

The cross product of the vectors (a₁, a₂, a₃) and (b₁, b₂, b₃) is given similarly by

$\det \begin{bmatrix} a_2 & a_3 \\ b_2 & b_3\end{bmatrix}\mathbf{i} - \det \begin{bmatrix} a_1 & a_3 \\ b_1 & b_3\end{bmatrix}\mathbf{j}%2B \det \begin{bmatrix} a_1 & a_2 \\ b_1 & b_2 \end{bmatrix} \mathbf{k}$

Thus the cross product may be computed by writing "symbolic determinant"

$\mathbf{a}\times\mathbf{b}=\det \begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{bmatrix}$

and expanding along the first row by rote, ignoring the fact that the matrix is not truly a matrix over the real or complex numbers (or whatever field the matrix entries belong to), and that thus the resulting computation does not compute an ordinary determinant. This is technically an abuse of notation, but is useful as a mnemonic to remember the formula for cross product and is very helpful in calculations.^[1]

Function application over set

John Harrison (1996)^[2] cites "the use of f(x) to represent both application of a function f to an argument x, and the image under f of a subset, x, of f's domain". (Note that the last x is usually written differently, e.g. as X, in order to distinguish an element x of the domain from a subset X.)

On the other hand, it is questionable that this is an abuse, since the definition of a function as an operator on subsets of the domain is widely known and is often stated explicitly in articles and books.

Exponentiation as repetition

Exponentiation is repeated multiplication, and multiplication is frequently denoted by juxtaposition of operands, with no operator at all. The suggested superscript notation for other associative operations denoted by juxtaposition follows:

Function application is sometimes denoted without parentheses: 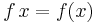$f\, x = f(x)$ . This suggests the functional powers notation: 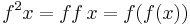$f^2 x = f f\, x = f(f(x))$ . This also generalizes nicely to represent function inverse for a power of -1 and functional square root for a power of 1/2.

Exponentiation over sets.

String repetition: "ab³c" = "abbbc".

Trigonometric functions

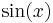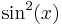In some countries it is common to denote the square of the value of $\sin(x)$ as $\sin^2(x)$ , and the inverse function as 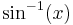$\sin^{-1}(x)$ . In his article on notation in the Edinburgh Encyclopedia Charles Babbage complains at length of this abuse of notation and suggests two alternatives for the notation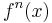 $f^n(x)$

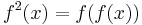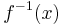Function composition, i.e. $f^2(x) = f(f(x))$ and $f^{-1}(x)$ is the inverse.
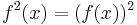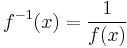Powers of the value, i.e. $f^2(x) = (f(x))^2$ and $f^{-1}(x)=\frac{1}{f(x)}$ is the reciprocal.

Babbage argues strongly for the former, and also that the square of the value should be notated as 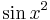$\sin x^2\$ , but beware: Babbage intends 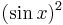$(\sin x)^2\$ even though what he wrote is easily confused with 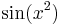$\sin(x^2)\$ (the only non-confusing way to avoid this abuse of notation is to always include the parentheses).

To press his example further, Babbage investigates what the function 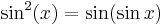$\sin^2(x) = \sin(\sin x)$ is like, and also 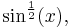$\sin^{\frac{1}{2}}(x),$ which is the function which, when composed with itself, equals 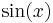$\sin(x)$ , the functional square root.

Big O notation

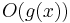With Big O notation, we say that some term $f(x)$ "is" $O(g(x))$ (given some function g, where x is one of f's parameters). Example: "Runtime of the algorithm is 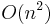$O(n^2)$ " or in symbols " 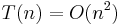$T(n) = O(n^2)$ ". Intuitively this notation groups functions according to their growth respective to some parameter; as such, the notation is abusive in two respects: It abuses "=", and it invokes terms that are real numbers instead of function terms. It would be appropriate to use the set membership notation and thus write 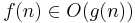$f(n)\in O(g(n))$ instead of 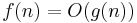$f(n)=O(g(n))$ . 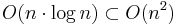This would allow for common set operations like $O(n\cdot\log n) \subset O(n^2)$ , $O(2^n) \bigcup O(n^2)$ , and it would make clear, that the relation is not symmetric in contrast to what the "=" symbol suggests. 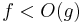Some argue for "=", because as an extension of the abuse, it could be useful to overload relation symbols such as < and ≤, such that, for example, $f < O(g)$ means that f's real growth is less than $g$ . But this further abuse is not necessary if, following Knuth one distinguishes between O and the closely related o and Θ notations. Concerning the use of terms for scalar numbers instead of functions, one encounters the following troubles.

You cannot cleanly define what 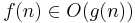$f(n)\in O(g(n))$ may mean, due to the fact the O notation is about growth of functions, but to the left hand and the right hand side of the relation, there are scalar values, and you cannot decide whether the relation holds if you look at particular function values.
The abused O notation is bound to one variable, and the identity of that variable can be ambiguous: for instance, in 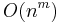$O(n^m)$ one of the variables might be a parameter which is not in scope of the $O$ .

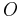That is, you might mean 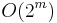$O(2^m)$ , since $n$ was the parameter that you assigned 2, or you might mean 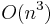$O(n^3)$ , since $m$ was the parameter substituted by 3 here.

Even 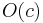$O(c)$ might be the same as 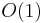$O(1)$ , since $c$ might be a parameter, not the concerned function variable.

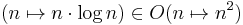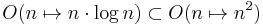The carelessness regarding the use of function terms might be caused by the rarely-used functional notations, like Lambda notation. You would have to write $(n\mapsto n\cdot\log n) \in O(n\mapsto n^2)$ and $O(n\mapsto n\cdot\log n) \subset O(n\mapsto n^2)$ . The correct O notation can be easily extended to complexity functions which map tuples to complexities; this lets you formulate a statement like "the graph algorithm needs time proportional to the logarithm of the number of edges and to the number of vertices" by 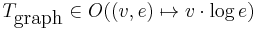$T_{\mbox{graph}}\in O((v,e)\mapsto v\cdot\log e)$ , which is not possible with the abused notation.

You can also state theorems like 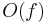$O(f)$ is a convex cone, and use that for formal reasoning.

Equality vs. isomorphism

Another common abuse of notation is to blur the distinction between equality and isomorphism. For instance, in the construction of the real numbers from Dedekind cuts of rational numbers, the rational number $r$ is identified with the set of all rational numbers less than $r$ , even though the two are obviously not the same thing (as one is a rational number and the other is a set of rational numbers). However, this ambiguity is tolerated, because the set of rational numbers and the set of Dedekind cuts of the form {x: x<r} have the same structure. It is through this abuse of notation that Q is regarded as a subset of R.

Sound pressure level

Sound pressure level measurements are commonly in dB(A) where the suffix "A" denotes A-weighting. There is ubiquitous misuse of "dB" in recording sound level measurements although a dB (decibel) is only a numerical ratio of two quantities.

Bourbaki

The term "abuse of language" frequently appears in the writings of Nicolas Bourbaki^[3]:

We have made a particular effort always to use rigorously correct language, without sacrificing simplicity. As far as possible we have drawn attention in the text to abuses of language, without which any mathematical text runs the risk of pedantry, not to say unreadability. Bourbaki (1988).

For example:

Let E be a set. A mapping f of E × E into E is called a law of composition on E. [...] By an abuse of language, a mapping of a subset of E × E into E is sometimes called a law of composition not everywhere defined on E. Bourbaki (1988).

In other words, it is an abuse of language to refer to partial functions from E × E to E as "functions from E × E to E that are not everywhere defined." To clarify this, it makes sense to compare the following two sentences.

1. A partial function from A to B is a function f: A' → B, where A' is a subset of A.

2. A function not everywhere defined from A to B is a function f: A' → B, where A' is a subset of A.

If one were to be extremely pedantic, one could say that even the term "partial function" could be called an abuse of language, because a partial function is not a function. (Whereas a continuous function is a function that is continuous.) But the use of adjectives (and adverbs) in this way is standard English practice, although it can occasionally be confusing. Some adjectives, such as "generalized", can only be used in this way. (e.g., a magma is a generalized group.)

The words "not everywhere defined", however, form a relative clause. Since in mathematics relative clauses are rarely used to generalize a noun, this might be considered an abuse of language. As mentioned above, this does not imply that such a term should not be used; although in this case perhaps "function not necessarily everywhere defined" would give a better idea of what is meant, and "partial function" is clearly the best option in most contexts.

Using the term "continuous function not everywhere defined" after having defined only "continuous function" and "function not everywhere defined" is not an example of abuse of language. In fact, as there are several reasonable definitions for this term, this would be an example of woolly thinking or a cryptic writing style.

Abuse of language or notation?

The terms "abuse of language" and "abuse of notation" depend on context. Writing "f: A → B" for a partial function from A to B is almost always an abuse of notation, but not in a category theoretic context, where f can be seen as a morphism in the category of partial functions.

References

^ Stewart, James (2007). Multivariable Calculus (6th ed.). Brooks/Cole. pp. 822–823. ISBN 0495011630.
^ Harrison, John (1996). "2.2 Criticism and reconstruction". Formalized Mathematics. Technical Reports 36. Turku Centre for Computer Science. ISBN 951-650-813-8. http://www.rbjones.com/rbjpub/logic/jrh0110.htm.
^ Bourbaki, Nicolas (1988). Algebra I: Chapters 1-3. Elements of Mathematics. Springer.

External links

"Strong Symbols", by Henning Thielemann (PDF Slides) Section 5: Common abuse of notation